2. 房价预测¶
本章使用PaddlePaddle深度学习框架,以房价预测为例,简单介绍下:
使用神经网络解决典型的机器学习:回归问题
如何使用paddlepaddle创建一个全连接神经网络
如何训练神经网络,介绍随机梯度下降等等
2.1. 线性神经网络¶
在机器学习中,线性回归(Linear Regression)最基础和最广泛应用的模型,是一种对自变量和因变量之间关系进行建模的回归分析,自变量数量 为1时称为简单回归,自变量数量大于1时称为多元回归。
将房价预测任务看作一个简单的线性回归问题,对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散的标签,区分为回归任务和分类任务, 因为房价是一个连续值,所以房价预测显然是一个回归任务。
我们以波士顿房价数据集(dataset)为例,该数据集统计了13种可能影响房价的因素和该类型房屋的均价。 下面假设房价和各影响因素之间能够用线性关系来描述:
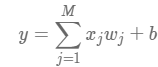
其中w是权重向量和b是偏置,模型的求解就是通过数据拟合出这两个参数;x是模型的输入,房价的影响因素;y是模型的输出,计算的房价。
我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络(计算层数时不考虑输入层), 用描述神经网络的方式来描述该线性模型,简单表示如下:
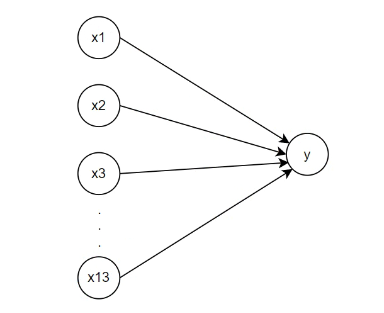
神经网络的标准结构中每个神经元由加权和与非线性变换构成,上图所示的神经网络单元中隐藏了权重,偏置和激活函数。 对于线性回归,每个输入都与每个输出(这里只有一个输出)相连,我们将这种变换称为 全连接层 (fully-connected layer)。
通过给定的波士顿房价数据集中包含的样本(这里是x1~x13总共13个影响房价的因素)和目标(或者说标签,其对应的是房价),经过训练计算出w和b的值, 这样就可以给定新的样本x时通过该模型计算出得出以一个目标值y,也就是我们要预测的房价。
那如何确认最佳的w和b,得到最好的预测房价?
需要通过一些算法实现,训练过程中需要衡量房价的预测值和数据集中真实值之间的误差,也就是 损失函数 (loss function), 回归问题中最常用的损失函数是平方误差函数。 而如何得到误差的最小化解,我们通过优化算法,房价预测使用的是 随机梯度下降法 (SGD)。
2.2. 训练房价预测模型¶
我们将尝试使用PaddlePaddle深度学习框架,基于波士顿房价数据集构建,训练一个简单的房价预测模型。 下面是构建深度学习神经网络的基础步骤(图片参考 这里 ):
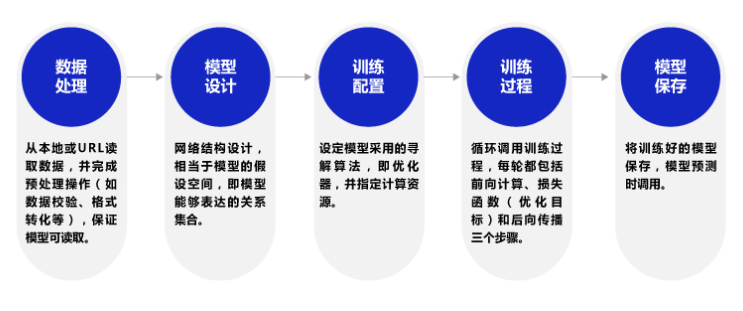
PaddlePaddle的安装:
# 使用conda创建一个名为paddle的环境,并指定python版本
conda activate
conda create -n paddle python=3.8
# 进入环境
conda activate paddle
# 安装最新版本的paddlepaddle计算平台是cpu(教程测试时最新版本是2.5.1)
conda install paddlepaddle==2.5.1 --channel https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/Paddle/
2.2.1. 数据处理¶
数据处理部分分为 导入数据, 数据变换, 数据集的划分 , 数据归一化处理 等操作。
导入数据,数据使用波士顿房价数据集,该数据集包含美国人口普查局收集的美国马萨诸塞州波士顿住房价格的有关信息, 数据集很小,只有506个案例, 可以从 这里 获取,该数据集有14个属性, 前面13个是可能影响房价的因素,最后一个是该类型房屋的均价。
数据变换,导入的数据是1维的,我们需要数据的形状进行变换,形成一个2维的矩阵(506行,14列),每行为一个数据样本(14个值), 每个数据样本包含13个影响房价的因素和一个该类型房屋的均价。
数据集的划分,将506组数据80%用作训练集,20%用于测试集,即其中404个样本数据是训练样本,102组数据作为测试样本。
数据归一化处理,将原始数据转换到[0 1]的范围内,这样使模型训练更高效等等。
数据处理的具体实现函数如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | def load_data():
# 使用numpy的fromfile,导入当前目录下的./data/housing.data数据
datafile = './data/housing.data'
data = np.fromfile(datafile, sep=' ', dtype=np.float32)
# 每条特征数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状,N =(data.shape[0] // 14), 其中"//"表示整除
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集,80%的数据做训练,20%的数据做测试,测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练数据集每一列的最大值,最小值(注意这里使用训练集的数据计算)
maximums, minimums = training_data.max(axis=0), training_data.min(axis=0)
# 记录数据的归一化参数
global max_values
global min_values
max_values = maximums
min_values = minimums
# 对数据进行归一化处理,线性变换将原始数据转换到[0 1]的范围,公式X=(x-min)/(max-min)
for i in range(feature_num):
data[:, i] = (data[:, i] - min_values[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例,然后返回两个划分的数据
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
|
2.2.2. 构建神经网络模型¶
通过前面的 线性神经网络 小节的简单分析,房价预测任务是一个简单的线性回归问题,并建立了一个简单模型,模型的输入特征是十三个影响房价的因素,预测值是房价。
这里测试使用paddlepaddle深度学习框架,先导入paddle一些子模块,其中paddle.nn下提供相关类和函数,包括线性变换层(Linear)、 二维卷积层(Conv2D)、长短期记忆网络LSTM、损失函数、ReLU激活层等等;paddle.nn.functional提供相关函数,包括激活函数、池化等等。 API接口的详细使用说明,请参考 飞浆的API文档 。
我们创建一个Regressor类,继承于paddle.nn.Layer 来自定义网络。其中 __init__ 是类的初始化函数,定义了一层全连接层,输入维度是13, 表示影响房价的十三个因素,输出维度是1,表示对应的房价。 接着定义一个 forward函数 (代表“前向计算”)完成从特征和参数到输出预测值的计算过程,返回本次任务中房价预测的结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | import paddle
from paddle.nn import Linear
import paddle.nn.functional as F
class Regressor(paddle.nn.Layer):
# 调用父类构造函数,声明一个全连接层
def __init__(self):
super(Regressor, self).__init__()
# 定义一层全连接层,输入维度是13,输出维度是1,是Linear类的实例
self.fc = Linear(in_features=13, out_features=1)
# 定义模型的前向传播,即如何根据输入X返回所需的模型输出
def forward(self, inputs):
x = self.fc(inputs)
return x
|
对于这个简单的网络模型,我们也可以直接使用实例化nn.Sequential,这样可以通过减少代码来快速完成模型构建:
1 | model = paddle.nn.Sequential(paddle.nn.Linear(13, 1))
|
在Sequential中添加的层将按照它们被添加的顺序执行,对Sequential模型进行前向传播时, 输入数据会按照添加到Sequential模型中的顺序依次经过每个层并得到输出。
2.2.3. 模型训练¶
在构建网络模型,设置超参数后,进入模型训练阶段,通过不断训练找到使损失函数最小化的模型参数值。训练结束后的参数, 我们可以用来评估测试,或者保存参数,将该模型保存下来。
训练使用随机梯度下降法(Stochastic Gradient Descent,SGD),每次从总的数据集中随机抽取出小部分数据来代表整体,基于这部分数据计算梯度和损失来更新参数。 一些参数解释:
mini_batche: 每次迭代时抽取出来的一批数据被称为一个mini-batch,在下面训练代码中就是变量mini_batches。
batch_size:一个mini-batch所包含的样本数目称为batch_size,在下面训练代码中就是参数BATCH_SIZE。
epoch:当程序迭代的时候,按mini-batch逐渐抽取出样本,当把整个数据集都遍历一遍,则完成了一轮训练,也叫一个epoch。在下面训练代码中就是参数EPOCH_NUM。
模型训练主要有两层循环(内层和外层循环)和单次训练的四个步骤(前向计算、损失函数计算、梯度计算、更新参数)。
外层循环,代表整个样本集合被训练遍历的次数,称为epoch,且每次循环前把样本数据随机打乱; 内层循环,代表每次遍历整个样本时,样本集合被拆分成的多个批次训练,然后全部执行训练。
前向计算,是将一个批次的样本数据灌入网络中,并计算输出结果;
计算损失函数,以前向计算结果和真实房价作为输入,通过损失函数square_error_cost 接口计算出损失函数值(Loss), 该接口具体使用参考下paddlepaddle的 API手册 ;
梯度计算,执行梯度反向传播backward函数,即从后到前逐层计算每一层的梯度,并根据设置的优化算法更新参数(opt.step函数);
更新参数,清空清空梯度变量,以备下一轮计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | # 声明网络结构
model = Regressor()
# 开启模型训练模式
model.train()
# 加载数据
training_data, test_data = load_data()
# 设置一些训练的参数
EPOCH_NUM = 10 # 循环整个训练数据集的次数
BATCH_SIZE = 10 # 设置batch大小,训练的批大小
# 定义优化算法,使用随机梯度下降算法SGD 学习率设置为0.01
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
# 在每轮迭代开始之前,将训练数据的顺序随机的打乱
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个batch包含10条数据
mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
# 定义内层循环
for iter_id, mini_batch in enumerate(mini_batches):
x = np.array(mini_batch[:, :-1]) # 获得当前批次训练数据,前面13列数据
y = np.array(mini_batch[:, -1:]) # 获得当前批次训练标签(真实房价),最后一列数据
# 将numpy数据转为tensor格式
house_features = paddle.to_tensor(x)
prices = paddle.to_tensor(y)
# 前向计算
predicts = model(house_features)
# 计算损失值,然后计算损失值的平均值avg_loss
loss = F.square_error_cost(predicts, label=prices)
avg_loss = paddle.mean(loss)
if iter_id%20==0:
print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.item()))
# 反向传播,计算每层参数的梯度值
avg_loss.backward()
# 更新参数,根据设置好的学习率迭代一步,最小化loss
opt.step()
# 清空梯度变量,以备下一轮计算
opt.clear_grad()
|
训练完成后保存模型:
1 2 3 | # 保存模型参数,文件名为LR_model.pdparams
paddle.save(model.state_dict(), './paddle/LR_model.pdparams')
print("模型参数保存在./paddle/LR_model.pdparams中")
|
2.2.4. 模型测试¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | # 数据集中抽一条样本作为测试样本
def load_one_example():
# 从上边已加载的测试集中,随机选择一条作为测试数据
idx = np.random.randint(0, test_data.shape[0])
one_data, label = test_data[idx, :-1], test_data[idx, -1]
# 修改该条数据shape为[1,13]
one_data = one_data.reshape([1,-1])
return one_data, label
# 导入模型参数文件
model_dict = paddle.load('./paddle/LR_model.pdparams')
model.load_dict(model_dict)
model.eval()
# 参数为数据集的文件地址
one_data, label = load_one_example()
# 将数据转为动态图的variable格式
one_data = paddle.to_tensor(one_data)
predict = model(one_data)
# 对结果做反归一化处理
predict = predict * (max_values[-1] - min_values[-1]) + min_values[-1]
# 对label数据做反归一化处理
label = label * (max_values[-1] - min_values[-1]) + min_values[-1]
# 打印测试结果
print("Inference result is {}, the corresponding label is {}".format(predict.numpy(), label))
|
