6. 简单组合逻辑 — 半加器¶
6.1. 章节导读¶
在上面两章节,我们设计并实现了简单组合逻辑中的多路选择器和3-8译码器,本章我们用Verilog语言描述一个具有半加器功能的电路,我们先从半加器作为引开始讲起,并在下一章中通过半加器构成的全加器来引入层次化设计的方法。
6.2. 理论学习¶
数字电路中加法器是经常用到的一种基本器件,主要用于两个数或者多个数的加和,加法器又分为半加器(half adder)和全加器(full adder)。半加器电路是指对两个输入数据位相加,输出一个结果位和进位,没有进位输入的加法器电路。是实现两个一位二进制数的加法运算电路。而全加器是在半加器的基础上的升级版,除了加数和被加数加和外还要加上上一级传进来的进位信号。
6.3. 实战演练¶
6.3.1. 实验目标¶
设计并实现一个半加器,使用开发板上的按键KEY1、KEY2作为被加数输入,选择开发板上的LED灯D6表示相加和的输出,LED灯D7表示进位输出。
6.3.2. 硬件资源¶
我们使用开发板上的按键和LED灯进行半加器的验证,选取KEY1、KEY2分别作为被加数in1、被加数in2的信号输入;以LED灯D6作为和的输出sum,以LED灯D7作为进位的输出count;如图 12‑1所示。
图 12‑1 硬件资源
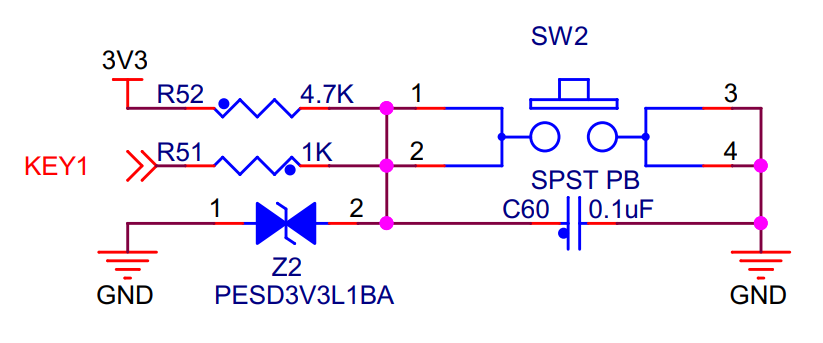
由原理图可知,征途Pro开发板的按键未按下时为高电平、按下后为低电平;LED灯则为低电平点亮。如图 12‑2、图 12‑3所示。
图 12‑2 按键部分原理图
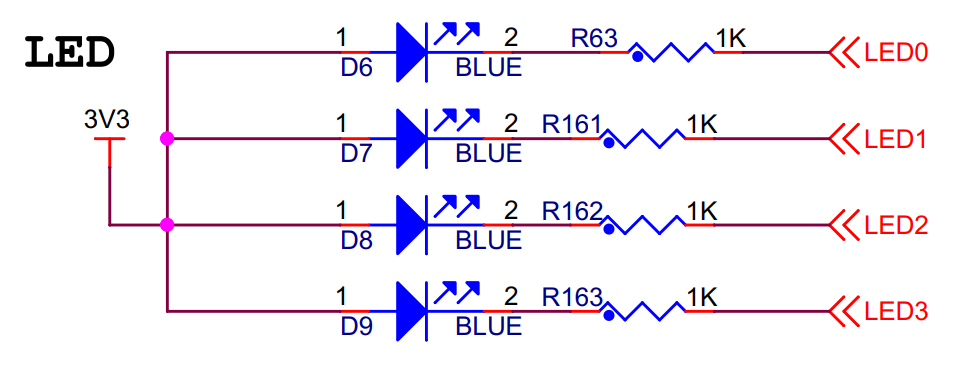
图 12‑3 LED灯原理图
6.3.3. 程序设计¶
6.3.3.1. 模块框图¶
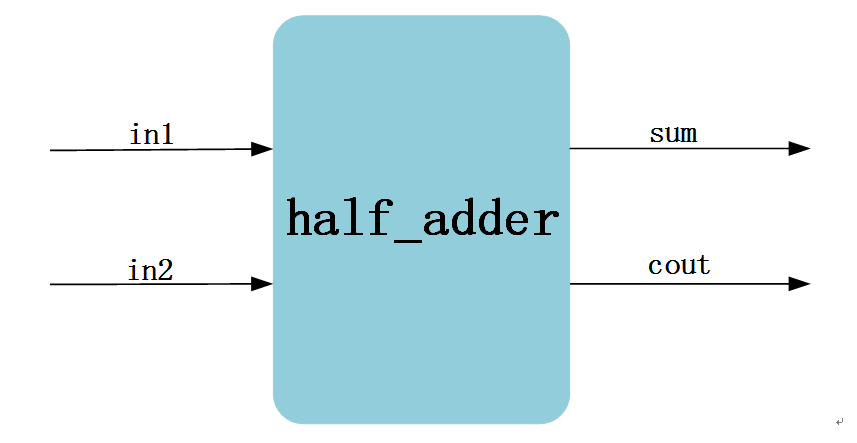
根据功能分析,该工程只需实现一个半加器的功能,所以设计成一个模块即可。模块命名half_adder,半加器由两个1bit的加数,分别命名为in1和in2,输出也有两个信号,为什么会是两个呢?我们不要忘记两个数加和后除了求得的“和”以外会有“进位”的情况,这里我们把进位信号单独拉出来,所以输出就有两个 信号,分别为1bit的sum和cout信号,该模块的功能是实现输入任意两个1bit加数的组合都能求得正确的和与进位值。根据上面的分析设计出的Visio框图如图 12‑4所示。
图 12‑4 模块框图
端口列表与功能总结如表格 12‑1所示。
表格 12‑1 输入输出信号描述
信号 |
位宽 |
类型 |
功能描述 |
|---|---|---|---|
in1 |
1Bit |
Input |
加数1 |
in2 |
1Bit |
Input |
加数2 |
sum |
1Bit |
Output |
两个加数的求和结果 |
cout |
1Bit |
Output |
两个加数求和后的进位信号 |
6.3.3.2. 波形图绘制¶
经分析得,in1和in2均为1bit输入信号,其任意组合有4种,就能够全覆盖验证所有的输入情况,这里我们任意画了4种输入情况,每种输入情况的组合根据相加的结果会对应输出4种求得的和与进位关系,我们根据这种关系可以轻松的列出如表格 12‑2所示的真值表,然后再根据真值表的输入与输出的对应关系画出波形图。其波形如图 12‑5所示,与真值表的关系一一对应。
表格 12‑2 半加器真值表
输入(input) |
输出(output) |
||
|---|---|---|---|
in1 |
in2 |
sum |
cout |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
图 12‑5 信号波形关系图
6.3.3.3. 代码编写¶
半加器参考代码如下所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | module half_adder
(
input wire in1 , //加数1
input wire in2 , //加数2
output wire sum , //两个数的加和
output wire cout //两个数加和后的进位
);
//sum:两个数加和的输出
//cout:两个数进位的输出
assign {cout, sum} = in1 + in2;
endmodule
|
根据上面RTL代码综合出的RTL视图如图 12‑6所示,我们可以看到加法器被抽象为一个“ADDER”的基本单元。
图 12‑6 RTL视图
6.3.3.4. 仿真验证¶
仿真文件编写
半加器仿真参考代码如下所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | `timescale 1ns/1ns
module tb_half_adder();
//reg define
reg in1;
reg in2;
//wire define
wire sum;
wire cout;
//初始化输入信号
initial begin
in1 <= 1'b0;
in2 <= 1'b0;
end
//in1:产生输入随机数,模拟加数1的输入情况
//取模求余数,产生随机数1'b0、1'b1,每隔10ns产生一次随机数
always #10 in1 <= {$random} % 2;
//in2:产生输入随机数,模拟加数2的输入情况
always #10 in2 <= {$random} % 2;
//------------------------------------------------------------
initial begin
$timeformat(-9, 0, "ns", 6);
$monitor("@time %t:in1=%b in2=%b sum=%b cout=%b",$time,in1,in2,sum,cout);
end
//------------------------------------------------------------
//--------------------half_adder_inst-----------------
half_adder half_adder_inst
(
.in1 (in1 ), //input in1
.in2 (in2 ), //input in2
.sum (sum ), //output sum
.cout (cout ) //output cout
);
endmodule
|
仿真波形分析
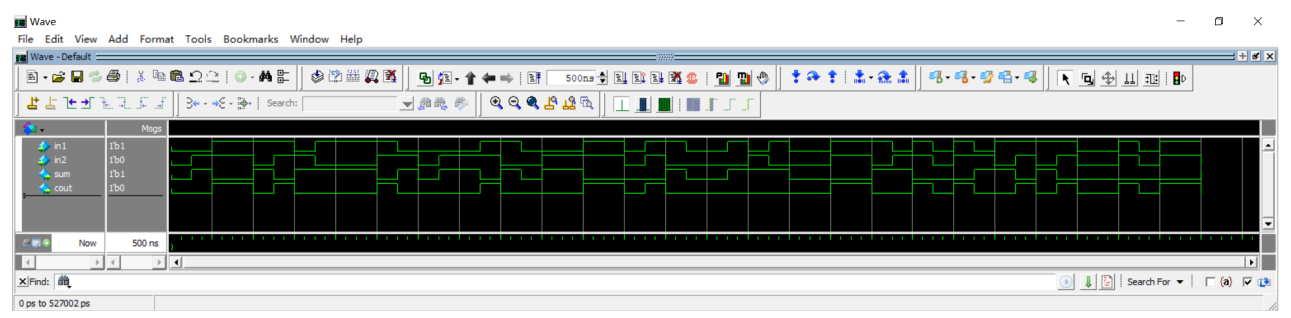
Testbench编写完成后,我们启动ModelSim进行功能仿真验证,同样我们也让波形跑了500ns,通过图 12‑7所示的波形我们可以观察到,in1和in2输入的值均为1bit随机数,而与之对应的sum和cout都是在输入变化的同一时刻立即变化,我们仔细核对每一组输入和输出之间的对应关系,发现波形中的“+”计算结果都是正确的,完全符合我们代码中的逻辑设计。
图 12‑7 仿真波形图
我们通过观察“Transcript”界面(如图 12‑8所示)中打印的结果发现与前面绘制真值表的结果一一对应,从而进一步验证了RTL代码设计的正确性。
图 12‑8 打印结果
6.3.4. 上板验证¶
6.3.4.1. 引脚约束¶
仿真验证通过后,准备上板验证,上板验证之前先要进行引脚约束。工程中各输入输出信号与开发板引脚对应关系如表格 12‑3所示。引脚配置如图 12‑9所示。
表格 12‑3 引脚分配表
信号名 |
信号类型 |
对应引脚 |
备注 |
|---|---|---|---|
in1 |
Input |
M2 |
按键 |
in2 |
Input |
M1 |
按键 |
sum |
Output |
L7 |
LED灯 |
count |
Output |
M6 |
LED灯 |
图 12‑9 引脚配置图
6.3.4.2. 结果验证¶
如图 12‑10所示,开发板连接12V直流电源和USB-Blaster下载器JTAG端口。线路正确连接后,打开开关为板卡上电。
图 12‑10 程序下载连线图
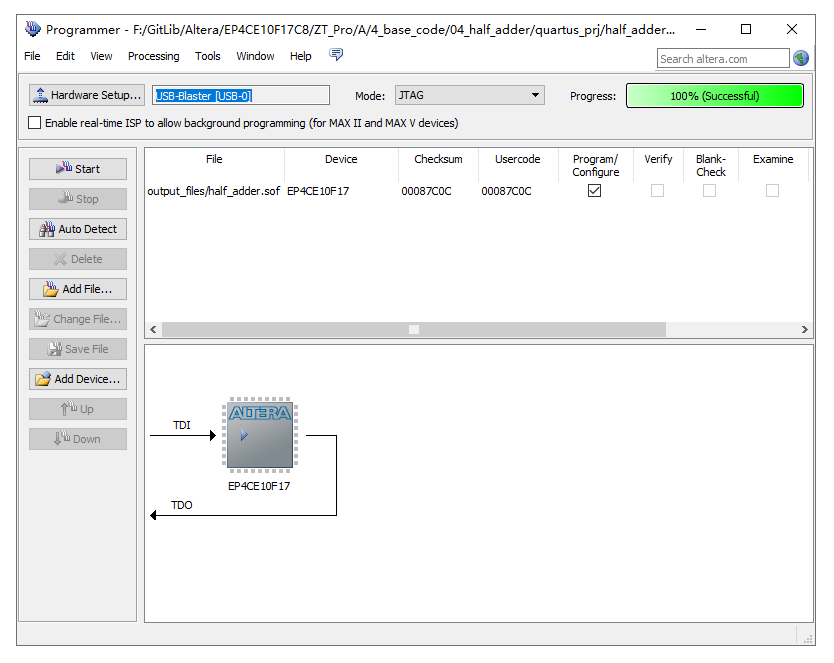
如图 12‑11所示,使用“Programmer”为开发板下载程序。
图 12‑11 程序下载窗口
程序下载完毕后,开始进行结果验证。如图 12‑12所示,当按键KEY1、KEY2同时按下,in1和in2输出均为低电平,得到和sum为0,进位count为0,D6、D7均被点亮。
图 12‑12 上板验证(一)
如图 12‑13、图 12‑14所示,只按下按键KEY1或KEY2,in1或in2输出低电平,得到和sum为1,进位count为0, D7被点亮。
图 12‑13 上板验证(二)
图 12‑14 上板验证(三)
如图 12‑15所示,两按键均未按下,in1和in2输出均为高电平,得到和sum为0,进位count为1,D6被点亮。
图 12‑15 上板验证(四)
6.4. 章末总结¶
本章主要讲解了数字电路中进行加法运算的基本加法单元——加法器,而我们设计的是一个没有前级进位功能且加数只有1bit的半加器,主要目的是为了引出下一章中的全加器。本章例子中所使用的语法和设计方法流程基本和之前相同,希望学习者能够进一步巩固开发方法和基本开发流程,认真完成章末的思考题。
新语法总结
重点掌握
+(最常用的数学运算符)
6.5. 拓展训练¶
尝试用always语句块的方式实现半加器;
我们在数电中往往通过真值表把组合逻辑化简成由与非门构成的最简电路形式,然后再根据表达式用Verilog语言实现。