17. 状态机

状态机大家一定都听说过，为什么需要状态机呢？通过前面章节的学习我们都知道FPGA是并行执行的，如果我们想要处理具有前后顺序的事件该怎么办呢？这时就需要引入状态机了。本章将从原理、实例、应用为大家总结了状态机设计和实现的方法。

17.1. 理论学习

状态机简写为FSM（Finite State Machine），也称为同步有限状态机，我们一般简称为状态机，之所以说“同步”是因为状态机中所有的状态跳转都是在时钟的作用下进行的，而“有限”则是说状态的个数是有限的。状态机根据影响输出的原因分为两大类，即Moore型状态机和Mealy型状态机，其共同点 是：状态的跳转都只和输入有关。区别主要是在输出的时候：若最后的输出只和当前状态有关而与输入无关则称为Moore型状态机；若最后的输出不仅和当前状态有关还和输入有关则称为Mealy型状态机。状态机是时序逻辑电路中非常重要的一个应用，常在大型复杂的系统中使用较多。

状态机的每一个状态代表一个事件，从执行当前事件到执行另一事件我们称之为状态的跳转或状态的转移，我们需要做的就是执行该事件然后跳转到一下时间，这样我们的系统就“活”了，可以正常的运转起来了。有研究显示状态机可以描述除相对论和量子力学以外的任何事情，但特别适合描述那些发生有先后顺序或时序规律的事情，在数 字电路系统中小到计数器大到微处理器都可以用状态机来进行描述。

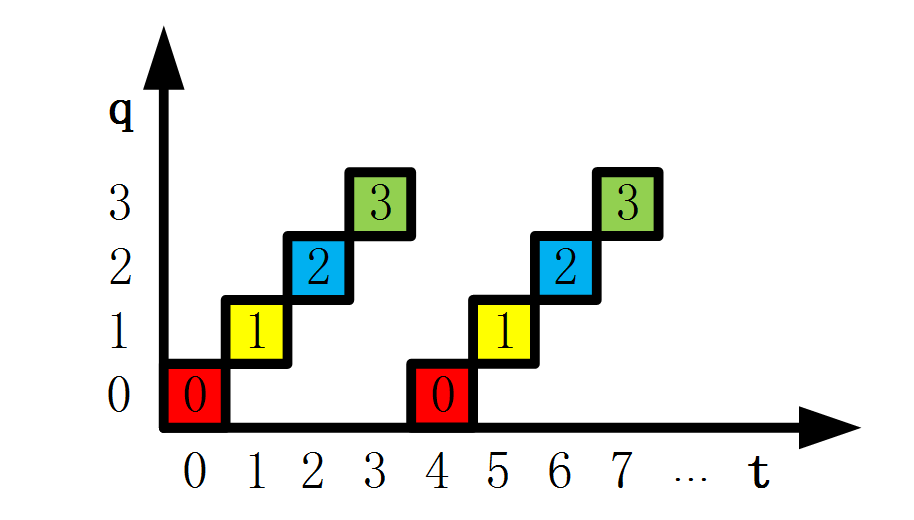
其实状态机也是一种函数关系，如图 23‑1所示，一个计数器其实就可以看作是一个最简单的状态机，输入是时钟信号，状态是计数的值，输出是计数的值，我们可以列出一个时间和输出的函数关系，函数表达式为q = counter(t)，坐标关系如图 23‑2所示，在有限的时间内，我们都可以根据具体的时间来算出当前输出的值是多少。

图 23‑1 计数器框图

图 23‑2 坐标关系图

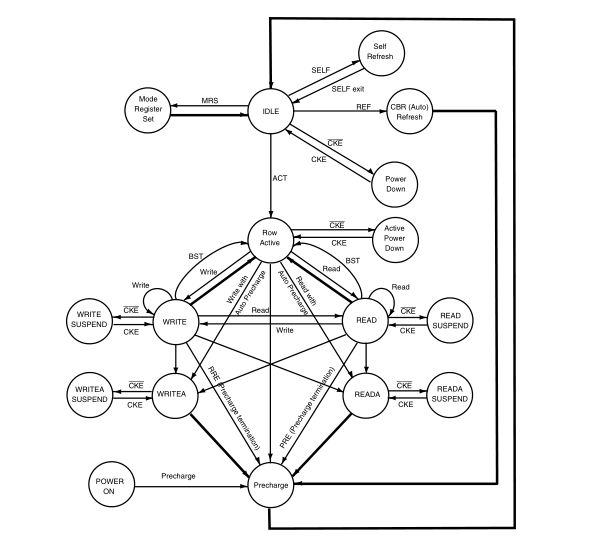
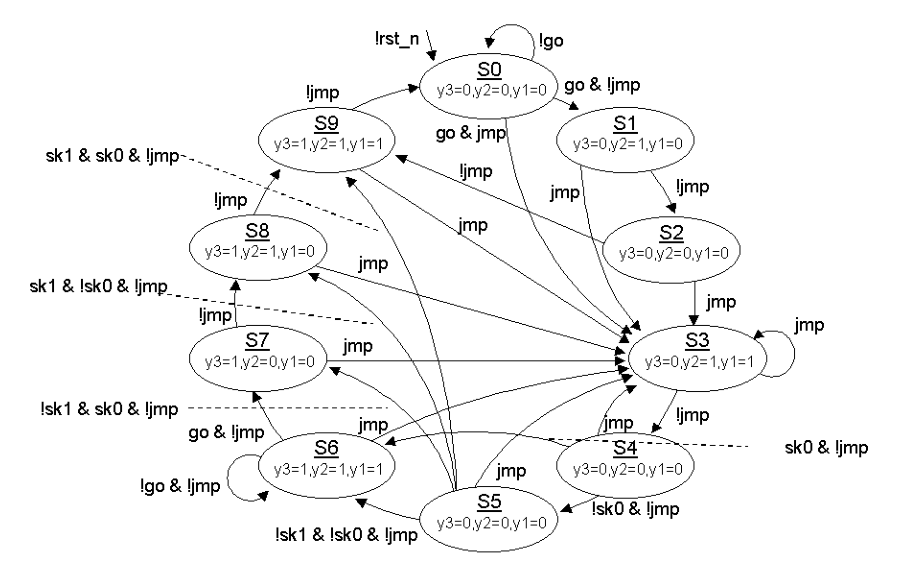
那么状态机该如何表示呢？我们会在一些数据手册中经常看到如图 23‑3和图 23‑4所示的图，这种图就是用于表达状态机的状态转移图。但是我们仔细观察发现这两个图也不是完全一样，但是都能够表达出状态和状态跳转的条件，这是状态转移图中最关键的因素，有了状态转移图，我们就可以对状态机想要表达的东西一清二楚， 包括用代码去实现都会变得很容易，所以说如何根据实际需求设计抽象出符合要求的状态机是非常关键的。本章我们会对如何从实际问题中抽象出状态转移图以及如何规范的绘制状态转移图以及如何根据状态转移图来设计代码做详细的讲解。

图 23‑3 状态转移图（一）

图 23‑4 状态转移图（二）

17.2. 实战演练一

我们知道状态机是怎么一回事儿了，下面我们就要学习如何用状态机来解决问题了。我们都在大街见过自动售卖饮料的可乐机，殊不知整个可乐机系统的售卖过程就可以很好的用状态机来实现，为了学习我们先来实现一个简单的可乐机系统。

17.2.1. 实验目标

可乐机每次只能投入1枚1元硬币，且每瓶可乐卖3元钱，即投入3个硬币就可以让可乐机出可乐，如果投币不够3元想放弃投币需要按复位键，否则之前投入的钱不能退回。

17.3. 程序设计

17.3.1. 模块框图

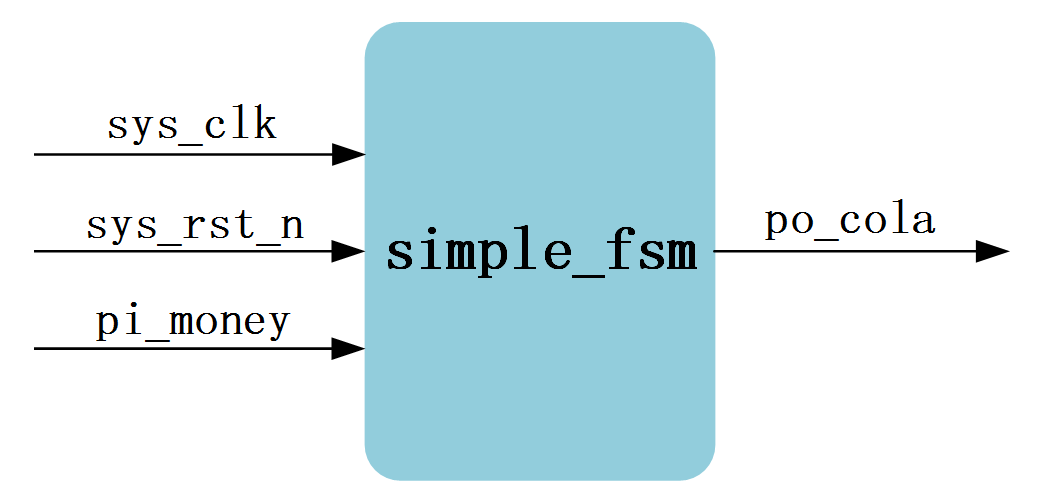
本例我们设计的是一个相对简单的状态机，而下一章我们会在此基础上添加一下功能，做一个稍微复杂的状态机，所以为了区别我们给本章的模块取名为simple_fsm。然后根据功能描述，我们大概可以分析出输入、输出有哪些信号。首先必不可少的是时钟和复位信号；其次是投币1元的输入信号，我们取名为pi_money； 可乐机输出我们购买的可乐，取名为po_cola。根据上面的分析设计出的Visio框图如图 23‑5所示。

图 23‑5 可乐机模块框图

端口列表与功能总结如表格 23‑1所示。

表格 23‑1 可乐机模块输入输出信号描述

信号	位宽	类型	功能描述
sys_clk	1Bit	Input	工作时钟，频率50MHz
sys_rst_n	1Bit	Input	复位信号，低电平有效
pi_money	1Bit	Input	投币1元的输入
po_cola	1Bit	Output	可乐的输出

17.3.1.1. 状态转移图与波形图绘制

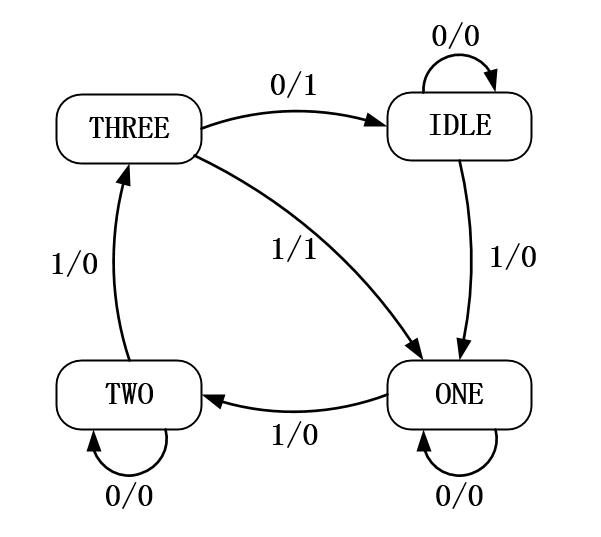
对于状态机的设计，其重点是状态转移图的设计，前面我们也列举了一些状态图，但没有统一的标准，有些只是为了表达一个系统，并不利于我们代码的编写和观察，所以我们有一个自己的规范标准，如图 23‑6所示，每个椭圆的框表示一个状态（也可以用其他图形表示），每个状态之间都有一个指向的箭头，表示的是状态跳转的过程，箭头上有标注的一组数字，斜杠左边表达的是状态的输入，斜杠右边表达的是状态的输出，结构非常的简单，各状态之间的功能、跳转的条件、输入输出都能够在状态转移图中非常清楚的表达出来。

图 23‑6 状态转移图规范标准

总结出来就是一个完整的状态转移图需要知道以下三个要素：

1、输入：根据输入可以确定是否需要进行状态跳转以及输出，是影响状态机系统执行过程的重要驱动力；

2、输出：根据当前时刻的状态以及输入，是状态机系统最终要执行的动作；

3、状态：根据输入和上一状态决定当前时刻所处的状态，是状态机系统执行的一个稳定的过程。

接下来我们套用上面的总结分析本例的状态转移图是如何绘制的。首先我们要将实际的问题抽象成我们需要的元素，就是要找到状态转移图所需要的输入、输出和状态分别对应着实际问题的哪些部分，分析结果如下：

1、输入：投入1元硬币；

2、输出：出可乐、不出可乐；

3、状态：可乐机中有0元、可乐机中有1元、可乐机中有2元、可乐机中有3元。

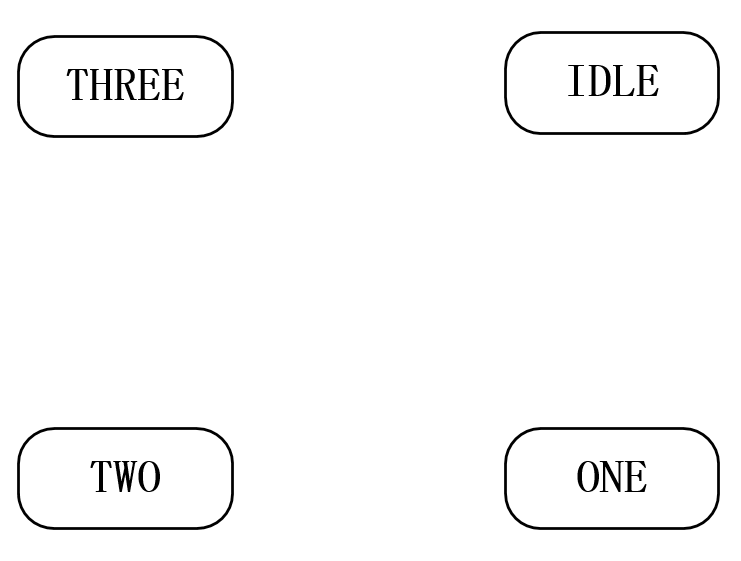
根据这些抽象出的要素我们就可以绘制状态转移图了，首先我们根据分析的状态数先画出4个状态，如图 23‑7所示，每个状态我们取一个有意义的名字，可乐机中有0元的状态是最原始的状态我们称之为IDLE状态，可乐机中有1元的状态我们就取名为ONE，可乐机中有2元的状态取名为TWO，可乐机中有3元的状态取名为THREE。

图 23‑7 可乐机状态图

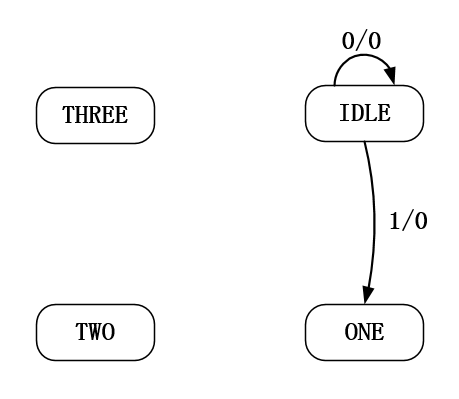
我们从第一个IDLE状态开始分析，从初使状态开始进行跳转。在IDLE状态下有两种情况，一种情况是我们什么也不干为0，状态还是继续维持在IDLE。另一种情况是我们投入1元钱，即在IDLE状态下的输入为1，此时并不会输出可乐，但是状态跳转到ONE状态了。初始状态IDLE的跳转只有以上分析的这两种情况，有 人可能还会说输入还有复位键呢，也会影响状态的跳转，为什么没有在状态转移图中表达呢？因为我们在代码中使用异步复位，执行复位操作后直接跳转到初始状态，所以不用在到状态转移图种单独表达。如图 23‑8所示。

图 23‑8 可乐机状态跳转（一）

接着我们该分析ONE状态跳转的情况了。在ONE状态下同样有两种情况，一种情况是你没有再继续投入1元钱，状态还是继续维持在ONE状态，可乐机等待新的1元钱投入，如果此时你不再继续投钱而选择离开，需要按一下复位按键回到初始状态等待下一个人从初始状态开始继续投币（代码中我们没有退回硬币的输出，只将状态机回 到初始状态），如果没有按复位下一个人可以继续在你之前投币的基础上继续计数。另一种情况是可乐机中已经有1元钱的情况下再投入1元钱，即在ONE状态下的输入为1，此时并不会输出可乐，所以在该状态下的输出为0，而状态则是跳转到TWO状态了。那么从ONE状态可以跳转的情况也只有两种，如图 23‑9所示。

图 23‑9 可乐机状态跳转（二）

下面我们该分析TWO状态跳转的情况了。在TWO状态下同样有两种情况，一种情况是你仍然没有再继续投入1元钱，状态还是继续维持在TWO状态，可乐机等待新的1元硬币投入，如果此时你不再继续投钱而选择离开需要按一下复位键回到初始状态，等待下一个人从初始状态开始投币。另一种情况是可乐机中已经有2元钱的情况下再 投入1元钱，即在TWO状态下的输入为1，需要特别注意了，这时可乐机中已经有3元钱了，是可以出可乐了，但是出了可乐后我们的状态应该是回到IDLE状态才正确，为什么又多出来一个THREE呢？很多同学在绘制状态转移图的时候往往在这里发现了问题，而把THREE状态去掉，变为图 23‑6所示的样子，这种最后优化为三种状态的状态转移图是正确的，那之前分析的四种状态的状态转移图是错误的吗？当然不是，我们继续把四种状态的状态转移图绘制完，再告诉大家为什么会有这种差别。

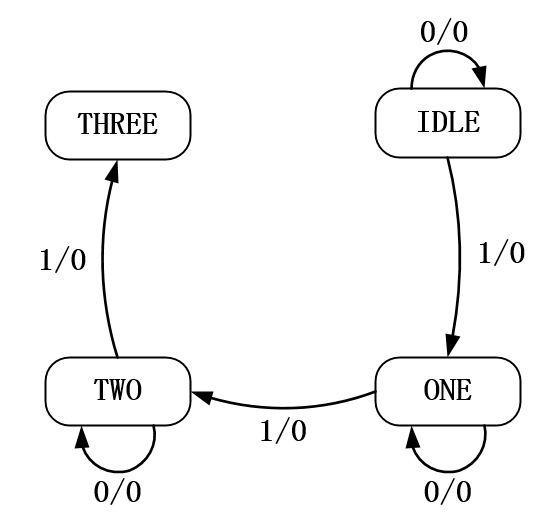
按照上面四种状态的状态转移图来分析，TWO状态下的第二种情况时虽然可乐机中有了3元钱，但是和上面分析不同的是可乐机器此时不会立刻出可乐，如图 23‑10所示，而是先跳转到THREE状态，等到了THREE状态的时刻，可乐机发现已经有人投了3元钱了，就不需要再投钱了，可以直接出可乐了。完整的状态转移图如图 23‑11所示。

图 23‑10 可乐机状态跳转（三）

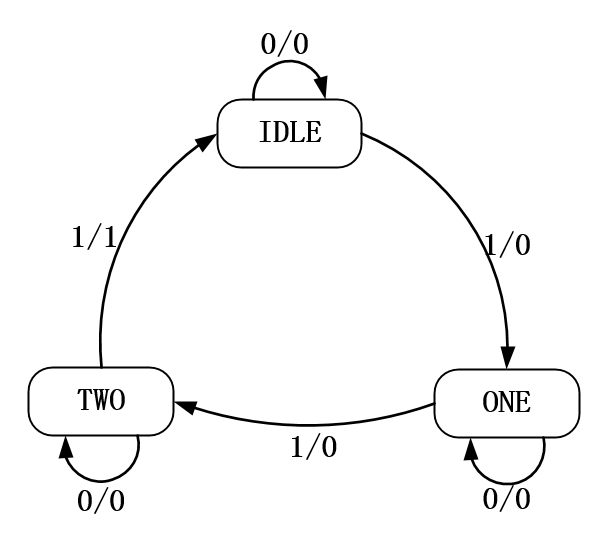
图 23‑11 完整可乐机状态转移图

有人可能会有疑问了，图 23‑6和图 23‑11这两种状态转移图都是对的吗？那就直白的告诉你这两种状态转移图都是对的，不要忘记了我们本节最开始讲到的状态机有两种，一种是Moore型状态机，一种是Mealy状态机，我们仔细看看这两种状态机的特点，最后的输出只和当前状态有关而与输入无关则称为Moore型状态机，图 23‑11所表达的状态转移图就是Moore型的。最后的输出不仅和当前状态有关还和输入有关则称为Mealy状态机，图 23‑6所表达的状态转移图就是Mealy型的。但是在最后设计的时候大家往往更喜欢把状态的个数化简到最简的状态，也有助于我们在代码实现的状态编码中节省相应的寄存器资源，所以后面我们按照图 23‑6所示的Mealy型状态机来讲解。

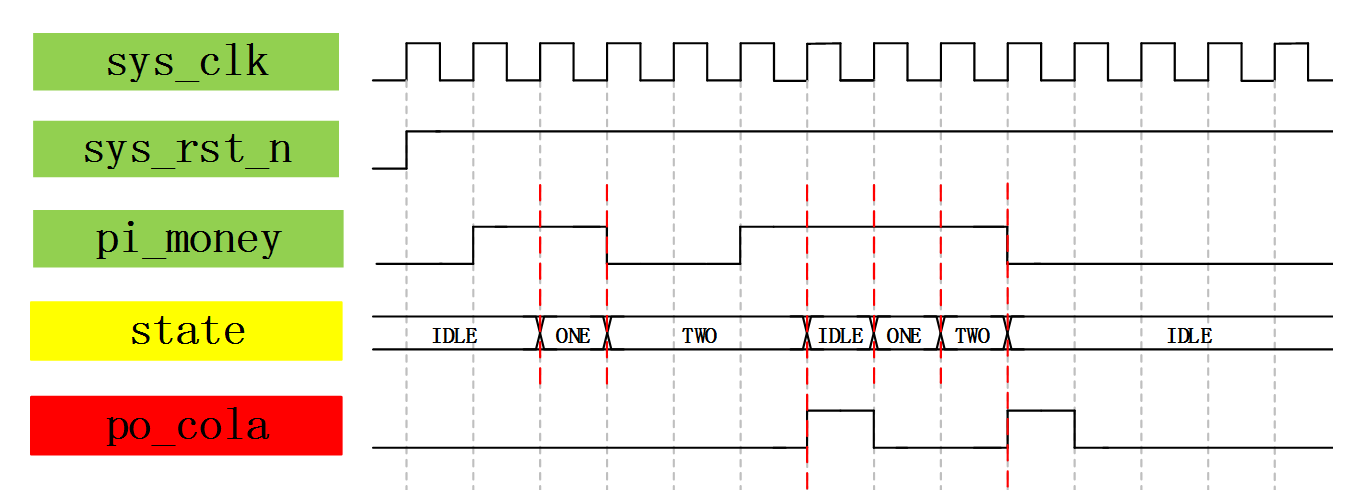
我们画波形图的目的就是为了写代码思路清晰，但是状态机比较特殊，我们根据实际的问题已经将状态转移图抽象出来了，根据状态转移图我们就可以很容易的实现状态机的RTL代码，在描述状态机时即使不绘制波形图也能够在写代码时有一个很清晰的思路。但是为了让大家能够更直观理解，这里我们还是将波形图画出，如图 23‑1 2所示，首先是三个输入信号，我们随机模拟输入信号pi_money的输入情况，根据状态转移图来分析继续绘制波形。因为有不同的状态之间的跳转关系，所以我们需要一个用于表示状态的变量，一般都取一个名为state的状态变量，state处于哪个状态、何时跳转都需要根据输入信号pi_money来决定，而输出信号 po_cola的结果则由输入pi_money和当前state的状态共同决定。

图 23‑12 状态机波形图

17.3.1.2. 代码编写

代码清单 23‑1 简单可乐机参考代码（simple_fsm）

module simple_fsm
(
input wire sys_clk , //系统时钟50MHz
input wire sys_rst_n , //全局复位
input wire pi_money , //投币方式可以为：不投币（0）、投1元（1）

output reg po_cola //po_cola为1时出可乐，po_cola为0时不出可乐

);

 ////
 //\* Parameter and Internal Signal \//
 ////

 //parameter define
 //只有三种状态，使用独热码
 parameter IDLE = 3'b001;
 parameter ONE = 3'b010;
 parameter TWO = 3'b100;

 //reg define
 reg [2:0] state ;

 ////
 //\* Main Code \//
 ////

 //第一段状态机，描述当前状态state如何根据输入跳转到下一状态
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 state <= IDLE; //任何情况下只要按复位就回到初始状态
 else case(state)
 IDLE : if(pi_money == 1'b1) //判断输入情况
 state <= ONE;
 else
 state <= IDLE;

 ONE : if(pi_money == 1'b1)
 state <= TWO;
 else
 state <= ONE;

 TWO : if(pi_money == 1'b1)
 state <= IDLE;
 else
 state <= TWO;
 //如果状态机跳转到编码的状态之外也回到初始状态
 default: state <= IDLE;
 endcase

 //第二段状态机，描述当前状态state和输入pi_money如何影响po_cola输出
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 po_cola <= 1'b0;
 else if((state == TWO) && (pi_money == 1'b1))
 po_cola <= 1'b1;
 else
 po_cola <= 1'b0;

 endmodule

上面是一个用Verilog描述的简单状态机，我们可以发现它是按照我们总结好的一套格式来编写的，我们按照这种格式再结合状态转移图可以编写出更复杂的状态机代码，所以我们总结一下我们套用的格式有哪些主要部分构成：其中01-09行是端口列表部分；17-19行是状态编码部；22行是定义的状态变量；29-49行 是第一段状态机部分；52-58是第二段状态机部分。一共有五部分，我们写状态机代码的时候根据这5部分对照着状态机依次编写，非常容易的就可以实现。

第一部分：第一部分是端口列表，和之前的设计一样没有什么特殊之处。

第二部分、第三部分：第二部分是状态编码，第三部分是状态变量，这两个是有联系的，所以放到一起讲解。17-19行是状态编码，状态转移图中有多少个状态数就需要有多少个状态编码，这里一共有3个状态数，所以就需要3个状态编码。22行是状态变量，这里为什么状态变量的位宽是3呢？因为我们采用了独热码的 编码方式，每个状态数只有1比特为1，其余比特都为0，所以3个状态就要用3位宽的变量，如果是4个状态那就要用4位宽的变量，也就是一共有几个状态数就需要几位宽的状态变量。那么除了用独热码的方式对状态进行编码，还有其他的方法吗？当然有，我们还可以采用二进制码或格雷码的方式对状态进行编码，上面的例子 中如果我们用二进制码编码3个状态则为：2’b00，2’b01，2’b10；而用格雷码编码3个状态则为：2’b00，2’b01，2’b11，都只需要2位宽的状态变量即可，即便是有4个状态数，我们使用2位宽的状态变量依然可以解决问题，要比独热码更节省状态变量的位宽个数。

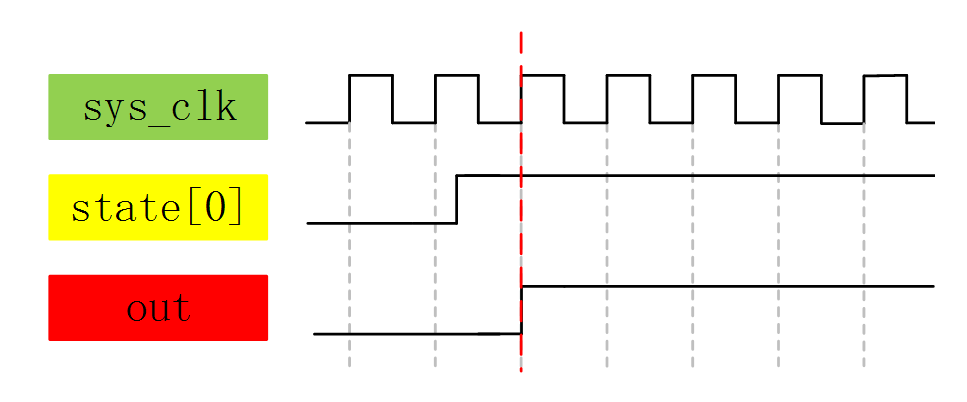
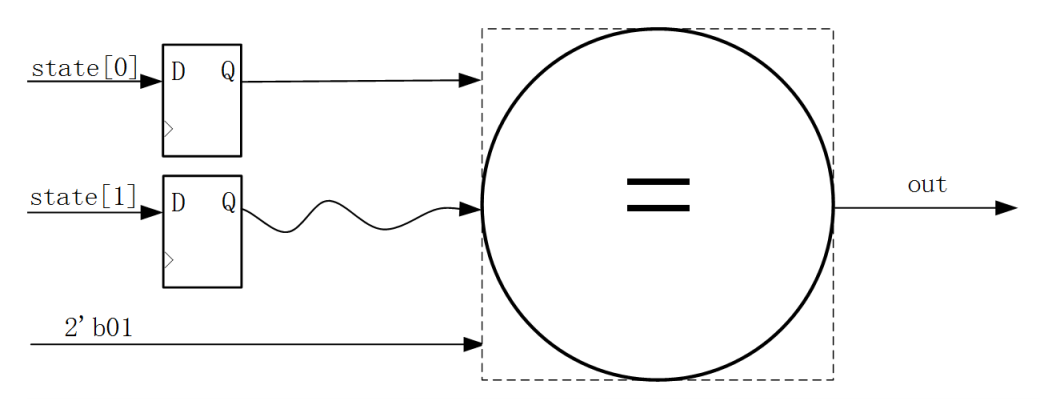
为什么例子中我们使用的是独热码而非二进制码或格雷码呢？那就要从每种编码的特性上说起了，首先独热码因为每个状态只有1bit是不同的，所以在执行到55行时的（state == TWO）这条语句时，综合器会识别出这是一个比较器，而因为只有1比特为1，所以综合器会进行智能优化为（state[2] == 1’ b1），这就相当于把之前3比特的比较器变为了1比特的比较器，大大节省了组合逻辑资源，但是付出的代价就是状态变量的位宽需要的比较多，而我们FPGA中组合逻辑资源相对较少，所以比较宝贵，而寄存器资源较多，所以很完美。而二进制编码的情况和独热码刚好相反，他因为使用了较少的状态变量，使之在减少了寄存器状态的 同时无法进行比较器部分的优化，所以使用的寄存器资源较少，而使用的组合逻辑资源较多，我们还知道CPLD就是一个组合逻辑资源多而寄存器逻辑资源少的器件，因为这里我们使用的是FPGA器件，所以使用独热码进行编码。就因为这个比较部分的优化，还使得使用独热码编码的状态机可以在高速系统上运行，其原因是多比特的比 较器每个比特到达比较器的时间可能会因为布局布线的走线长短而导致路径延时的不同，这样在高速系统下，就会导致采集到不稳定的状态，导致比较后的结果产生一个时钟的毛刺，使输出不稳定，而单比特的比较器就不用考虑这种问题。下面是示意图解析。

图 23‑13 单比特比较器示意图

图 23‑14 单比特比较器波形图

图 23‑15 多比特比较器示意图

图 23‑16 低通系统下多比特比较器波形图

图 23‑17 高速系统下多比特比较器波形图

用独热码编码虽然好处多多，但是如果状态数非常多的话即使是FPGA也吃不消独热码对寄存器的消耗，所以当状态数特别多的时候可以使用格雷码对状态进行编码。格雷码虽然也是和二进制编码一样使用的寄存器资源少，组合逻辑资源多，但是其相邻状态转换时只有一个状态发生翻转，这样不仅能消除状态转换时由多条信号线的传输延 迟所造成的毛刺，又可以降低功耗，所以要优于二进制码的方式，相当于是独热码和二进制编码的折中。

最后我们用一个表格来总结一下什么时候使用什么方式的编码效果最好（有时候不管你使用哪种编码方式，综合器会根据实际情况在综合时智能的给你进行编码的转换，当然这需要你设置额外的综合约束，这里我们不再详细讲解）。

表格 23‑2 编码方式表

CPLD器件	FPGA器件
低速系统	高速系统	低速系统	高速系统
状态个数	状态个数	状态个数	状态个数
<4	4-24	>24	所有状态	<4	4-24	>24	所有状态
独热码	二进制码	格雷码	独热码	二进制码	独热码	格雷码	独热码

第四部分和第五部分：第四部分和第五部分也是有联系的，也是状态机中最为关键的部分，综合器能不能将RTL代码综合为状态机的样子主要看这部分代码如何来实现的。大家看到我们的代码使用的是二段式状态机，但是又感觉怪怪的，我们描述的状态机之所以和其他资料上的有所区别，其实我们是使用了新的写法。很多人 都见过其他资料上总结的状态机代码写法有一段式、二段式、三段式（一段式指的是在一段状态机中使用时序逻辑既描述状态的转移，也描述数据的输出；二段式指在第一段状态机中使用时序逻辑描述状态转移，在第二段状态机中使用组合逻辑描述数据的输出；三段式指在第一段状态机中采用时序逻辑描述状态转移，在第二段在状态机中采 用组合逻辑判断状态转移条件描述状态转移规律，在第三段状态机中描述状态输出，可以用组合电路输出，也可以时序电路输出）。这种一段式、二段式、三段式其实都是之前经典的老写法，也是一些老工程师仍然习惯用的写法，老方法是根据状态机理论建立的模型抽象后设计的，其实要严格按照固定的格式来写代码，否则综合器将无法识 别出你写的代码是个状态机，因为早期的开发工具只能识别出固定的状态机格式，如果不按照标准格式写代码综合器最后无法综合成为状态机的样子。这样往往增加了设计的难度，很多人学习的时候还要去了解理论模型，反复学习理解很久才能够设计好的状态机，所以需要我们改进。

老的一段式、二段式、三段式各有优缺点，其中一段式在描述大型状态机时会比较困难，会使整个系统显得十分臃肿，不够清晰；二段式状态机的好处是其结构和理想的理论模型完全吻合，即不会有附加的结构存在，比较精简，但是由于二段状态机的第二段是组合逻辑描述数据的输出，所以有一些情况是无法描述的，比如输出时需要类似计 数的累加情况，这种情况在组合逻辑中会产生自迭代，自迭代在组合逻辑电路中是严格禁止的，而且第二段状态机主要是描述数据的输出，输出时使用组合逻辑往往会产生更多的毛刺，所以并不推荐。所以衍生出三段式状态机，三段状态机的输出就可是时序逻辑了，但是其结构并不是最精简的了。三段式状态机的第一段状态机是用时序逻辑 描述当前状态，第二段状态机是用组合逻辑描述下一状态，如果把这两个部分进行合并而第三段状态机保持不变，就是我们现在最新的二段式状态机了。这种新的写法在现在不同综合器中都可以被识别出来，这样既消除了组合逻辑可能产生的毛刺，又减小了代码量，还更加容易上手，不必再去关心理论模型是怎样的，仅仅根据状态转移图就 非常容易实现，对初学者来说十分友好。所以我们习惯性的使用两个均采用时序逻辑的 always 块，第一个 always 块描述状态的转移为第一段状态机，第二个 always 块描述数据的输出为第二段状态机（如果我们遵循一个always块只描述一个变量的原则，如果有多个输出时第二段状态机就可以分为多个always块来表达，但理论上仍属于新二段状态机，所以几段式状态机并不是由always块的数量简单决定的）。

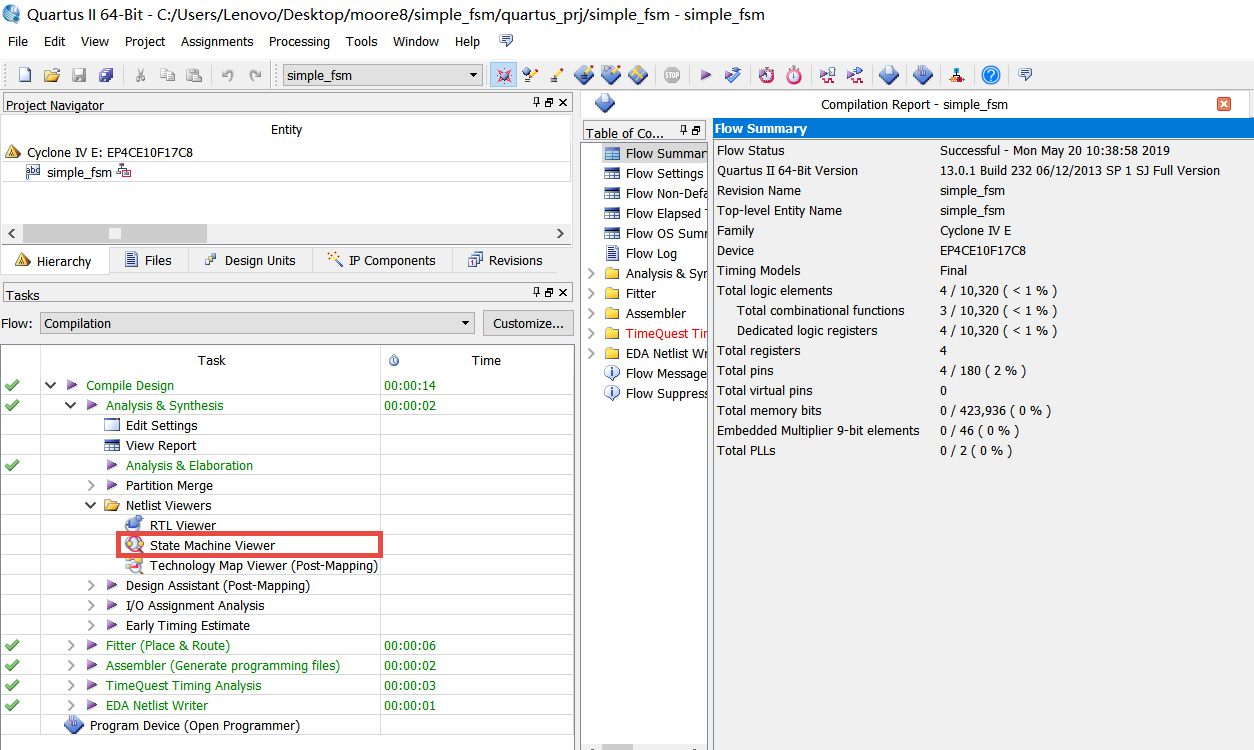
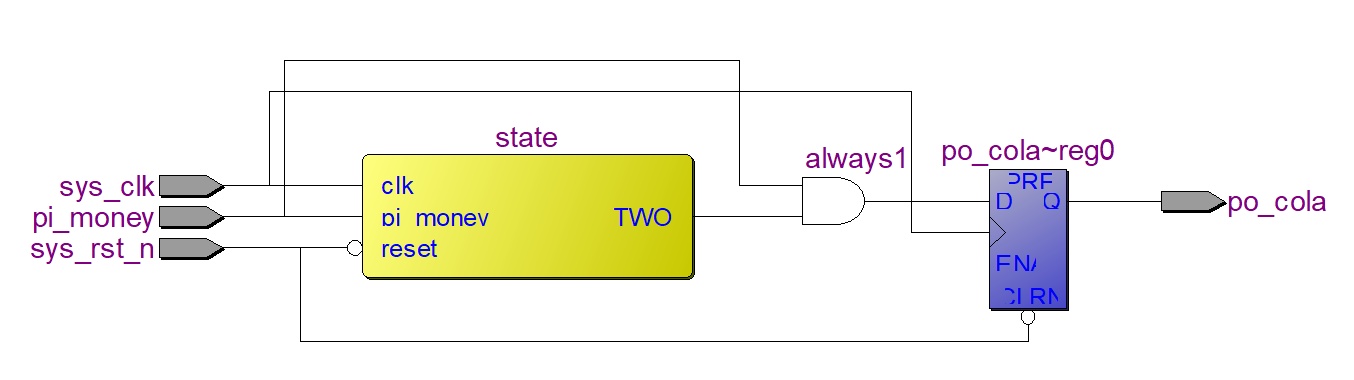
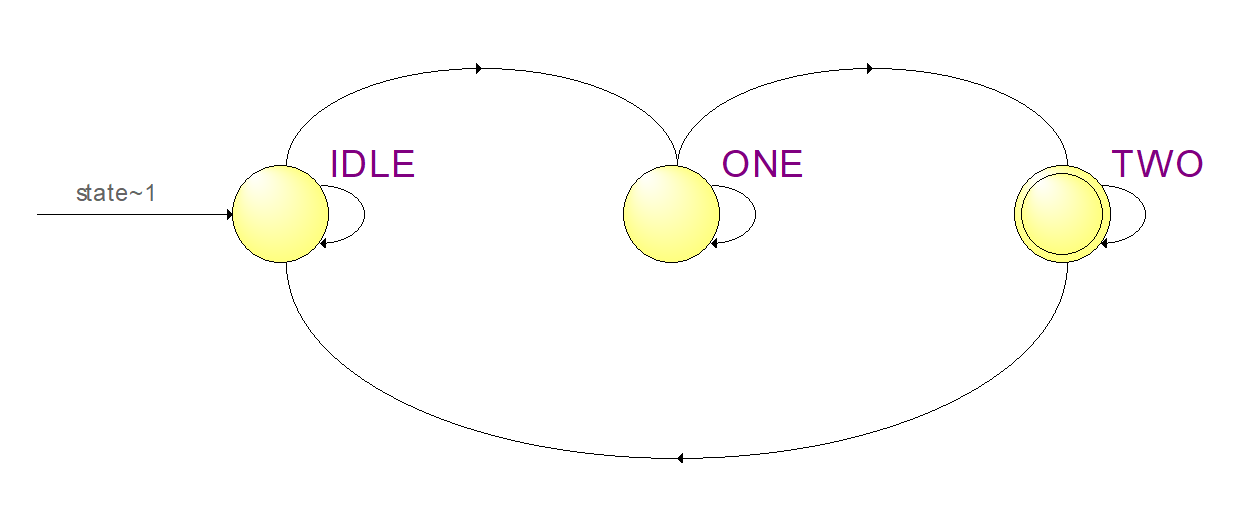
如果我们写的是状态机，综合器是可以识别出来的，如图 23‑18所示选择双击“Netlist Viewers”下的“State Machine Viewer”或者打开RTL视图的时候看到如图 23‑19所示的黄色块就是综合器自动识别出的状态机，双击进去也可以查看状态转移图，打开后显示的状态转移图如图 23‑20所示。

图 23‑18 状态机查看

图 23‑19 RTL视图

图 23‑20 状态转移图

17.3.1.3. 仿真验证

仿真文件编写

为了方便观察状态的跳转，我们在仿真中加入了需要查看的信息并打印出来。

代码清单 23‑2 简单可乐机仿真参考代码（tb_simple_fam.v）

\`timescale 1ns/1ns
module tb_simple_fsm();

////
//\* Parameter and Internal Signal \//
////

//reg define
reg sys_clk ;
 reg sys_rst_n ;
 reg pi_money ;

 //wire define
 wire po_cola;

 ////
 //\* Main Code \//
 ////

 //初始化系统时钟、全局复位
 initial begin
 sys_clk = 1'b1;
 sys_rst_n <= 1'b0;
 #20
 sys_rst_n <= 1'b1;
 end

 //sys_clk:模拟系统时钟，每10ns电平翻转一次，周期为20ns，频率为50MHz
 always #10 sys_clk = ~sys_clk;

 //pi_money:产生输入随机数，模拟投币1元的情况
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 pi_money <= 1'b0;
 else
 pi_money <= {$random} % 2; //取模求余数，产生非负随机数0、1

 //------------------------------------------------------------
 //将RTL模块中的内部信号引入到Testbench模块中进行观察
 wire [2:0] state = simple_fsm_inst.state;

 initial begin
 $timeformat(-9, 0, "ns", 6);
 $monitor("@time %t: pi_money=%b state=%b po_cola=%b",
 $time, pi_money, state, po_cola);
 end
 //------------------------------------------------------------

 ////
 //\* Instantiation \//
 ////

 //------------------------simple_fsm_inst------------------------
 simple_fsm simple_fsm_inst(
 .sys_clk (sys_clk ), //input sys_clk
 .sys_rst_n (sys_rst_n ), //input sys_rst_n
 .pi_money (pi_money ), //input pi_money

 .po_cola (po_cola ) //output po_cola
 );

 endmodule

这里我们需要对第40行代码进行额外的补充讲解，在之前的章节中大家没有见到过这种用法。第40行重新定义了一个2bit名为state的变量（该变量也可以是其他名字，这里我们为了观察方便，所以该变量名尽量和RTL模块中的名字一致），然后通过在Testbench模块中实例化RTL模块的名字与“.”定位到RT L模块中的信号，如果要引入到Testbench模块中的信号是RTL模块多层实例化中最底层的信号则需要从顶层的实例化RTL模块的名字与“.”依次传递，直到最后定位到内部的信号。这样我们就把RTL模块中的内部信号引入到Testbench模块中了。之所以这样做是因为我们要在ModelSim的“Transc ript”界面中打印RTL模块中内部信号的信息以方便观察验证，直接实例化RTL模块的方式只能够将RTL模块中的端口信号引入到Testbench模块中，而不能将RTL模块的内部信号引入到Testbench模块中，所以无法在ModelSim的“Transcript”界面中观察打印的信息。

仿真波形分析

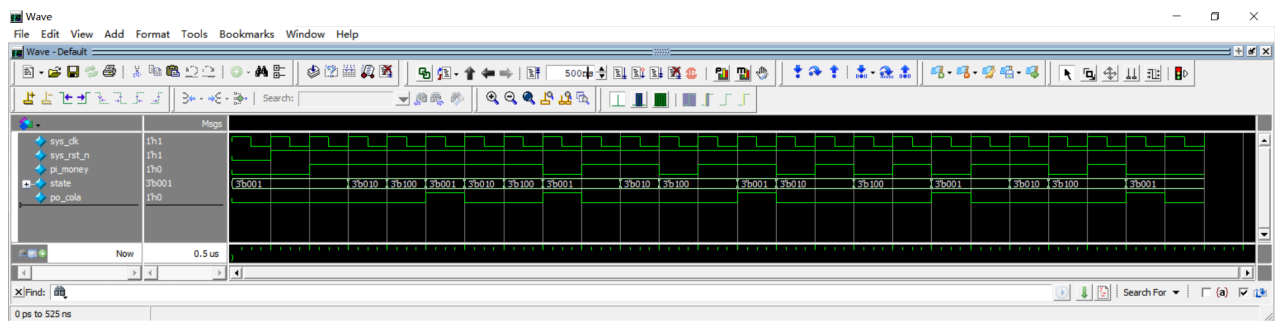
打开ModelSim执行仿真，仿真出来的波形如图 23‑21所示，我们让仿真运行了500ns，可以看到输出信号po_cola是根据输入信号pi_money和状态变量state共同影响变化的，对照状态转移图和波形图，发现是完全一致的，验证正确。

图 23‑21 仿真波形图

我们在观察状态机的波形时要根据输入信号pi_money和状态变量state一起来观察输出信号po_cola的状态，不是很直观，需要一个个的数，这时我们想起了之前通过观察“Transcript”界面打印的信息来观察信号的方式，在Testbench模块中我们也添加了相应的代码，且可以看到我们在Testb ench模块中引入的RTL模块中内部信号state的信息，仿真结果如图 23‑22所示，阅读“Transcript”界面打印的信息时不要忘记时序逻辑电路延一拍的特点。

图 23‑22 打印信息

17.4. 实战演练二

上一部分中的可乐机比较简单，只能投1元的硬币，但是我们生活中还有0.5元的硬币，所以我们在本章中将可乐机设计的稍微复杂一些，做成既可以投1元的硬币也可以投0.5元的硬币，然后我们把可乐的定价改为2.5元一瓶。我们增加了可乐机的复杂度而引入了新的问题：投币后可乐机不仅仅需要吐出可乐还有可能出现需要找零 钱的情况。这样我们的设计就更加有意思了，也更加符合真实的情况了。

17.4.1. 实验目标

可乐定价为2.5元一瓶，可投入0.5元、1元硬币，投币不够2.5元需要按复位键退回钱款，投币超过2.5元需找零。

17.5. 程序设计-1

17.5.1. 模块框图-1

本例我们设计一个相对上一节简单状态机较复杂的状态机，该例子和上一节所解决的问题是类似的，但是输入和输出都增加了新的内容，所以我们给本章的模块取名为complex_fsm。根据功能描述，我们可以分析出输入、输出有哪些信号。首先时钟和复位信号依然是必不可少的输入信号；输入信号还有投币，除了可以投1元外， 还可以投0.5元，所以我们将投币1元的输入信号取名为pi_money_one，将投币0.5元的输入信号取名为pi_money_half；可乐机的输出除了可乐还可能会有找零（找零的结果只有一种即找回0.5元），我们将可乐机输出购买可乐的信号取名为po_cola，找零的信号取名为po_money。根据上 面的分析设计出的Visio框图如图 23‑23所示。

图 23‑23 可乐机模块框图

端口列表与功能总结如表格 23‑3所示。

表格 23‑3 可乐机模块输入输出信号描述

信号	位宽	类型	功能描述
sys_clk	1Bit	Input	工作时钟，频率50MHz
sys_rst_n	1Bit	Input	复位信号，低电平有效
pi_money_one	1Bit	Input	投币1元的输入
pi_money_half	1Bit	Input	投币0.5元的输入
po_cola	1Bit	Output	可乐的输出
po_money	1Bit	Output	找零的输出

17.5.1.1. 状态转移图与波形图绘制

在绘制状态转移图时我们仍套用上一节中的三要素法来分析。首先我们要将实际的问题抽象成我们需要的元素，找到实际问题中对应状态转移图所需要的输入、输出和状态的部分，分析结果如下：

1、输入：投入0.5元硬币、投入1元硬币；

2、输出：不出可乐/不找零、出可乐/不找零、出可乐/找零；

3、状态：可乐机中有0元、可乐机中有0.5元、可乐机中有1元、可乐机中有1.5元、可乐机中有2元、可乐机中有2.5元、可乐机中有3元。

根据这些抽象出的要素我们就可以绘制状态转移图了，这里我们需要格外注意的是输入和输出都不再是一个信号，而是两个信号，而在表达状态转移图中状态跳转的条件时依然只能是斜杠左边为输入，斜杠右边为输出，这也就意味着我们要将输入的多个信号编为一组，输出的多个信号编为一组，然后再进行量化编码，编码方式自定义，只要 不冲突即可。所以输入我们将不投币、只投入0.5元、投入1元的情况分别编码为00、01、10，；输出我们将不出可乐不找零、只出可乐、既出可乐又找零的情况（不存在只找零不出可乐的情况）分别编码为00、10、11，下面就可以绘制状态转移图了。

首先我们根据分析的状态数先画出7个状态，每个状态我们取一个有意义的名字，我们还是和上一节的分析方法一样，从IDLE初始状态开始分析，把每一个状态的输入和跳转情况考虑完整，再去分析下一个状态，全部分析结束后，我们使用Mealy型状态机的表达方式将其化简到最少状态，最终绘制出的状态转移图如图 23‑24所示。

图 23‑24 复杂可乐机状态转移图

大家在画状态转移图时容易出现状态跳转情况遗漏的问题，这里我们给大家总结一个小技巧：我们可以观察到，输入有多少种情况（上一节是两种输入情况，本节是三种输入情况），每个状态的跳转就有多少种情况（上一节每个状态都有两种跳转情况，本节每个状态都有三种跳转情况），这样根据输入来确定状态的跳转就能够保证我们不漏 掉任何一种状态跳转。

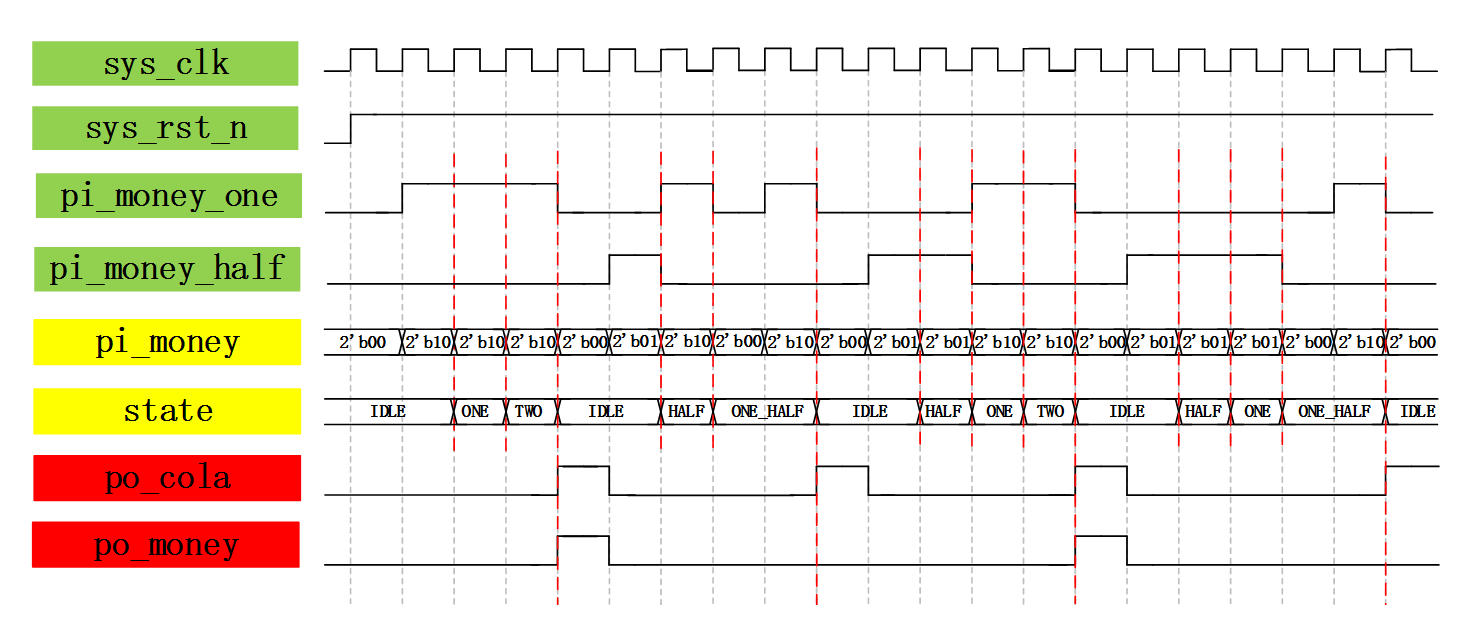
我们根据状态转移图将波形图画出，首先是四个输入信号，我们随机模拟输入信号pi_money_one和pi_money_half的输入情况，为了和状态转移图的输入信号编码对应且方便观察（写代码时也方便）我们将输入信号pi_money_one和pi_money_half组合到一起，取一个名为pi_mone y的中间变量。然后再画出用于表示状态的状态变量state，根据输入信号pi_money和状态变量state确定输出信号po_cola和po_money的波形，输出信号我们就不用再进行组合了单独输出即可。绘制好的波形图如图 23‑25所示。

图 23‑25 状态机波形图

17.5.1.2. 代码编写

代码清单 23‑3 复杂可乐机参考代码（complex_fsm.v）

module complex_fsm
(
input wire sys_clk , //系统时钟50MHz
input wire sys_rst_n , //全局复位
input wire pi_money_one , //投币1元
input wire pi_money_half , //投币0.5元

output reg po_money , //po_money为1时表示找零
//po_money为0时表示不找零
output reg po_cola //po_cola为1时出可乐
//po_cola为0时不出可乐
);
////
//\* Parameter and Internal Signal \//
////
//parameter define
//只有五种状态，使用独热码
parameter IDLE = 5'b00001;
parameter HALF = 5'b00010;
parameter ONE = 5'b00100;
parameter ONE_HALF = 5'b01000;
parameter TWO = 5'b10000;
//reg define
reg [4:0] state;
//wire define
wire [1:0] pi_money;
////
//\* Main Code \//
////
//pi_money:为了减少变量的个数，我们用位拼接把输入的两个1bit信号拼接成1个2bit信号
//投币方式可以为：不投币（00）、投0.5元（01）、投1元（10），每次只投一个币
assign pi_money = {pi_money_one, pi_money_half};
//第一段状态机，描述当前状态state如何根据输入跳转到下一状态
always@(posedge sys_clk or negedge sys_rst_n)
if(sys_rst_n == 1'b0)
state <= IDLE; //任何情况下只要按复位就回到初始状态
else case(state)
IDLE : if(pi_money == 2'b01) //判断一种输入情况
state <= HALF;
else if(pi_money == 2'b10)//判断另一种输入情况
state <= ONE;
else
state <= IDLE;
HALF : if(pi_money == 2'b01)
state <= ONE;
else if(pi_money == 2'b10)
state <= ONE_HALF;
else
state <= HALF;
ONE : if(pi_money == 2'b01)
state <= ONE_HALF;
else if(pi_money == 2'b10)
state <= TWO;
else
state <= ONE;
ONE_HALF: if(pi_money == 2'b01)
state <= TWO;
else if(pi_money == 2'b10)
state <= IDLE;
else
state <= ONE_HALF;
TWO : if((pi_money == 2'b01) \|\| (pi_money == 2'b10))
state <= IDLE;
else
state <= TWO;
//如果状态机跳转到编码的状态之外也回到初始状态
default : state <= IDLE;
endcase
//第二段状态机，描述当前状态state和输入pi_money如何影响po_cola输出
always@(posedge sys_clk or negedge sys_rst_n)
if(sys_rst_n == 1'b0)
po_cola <= 1'b0;
else if((state == TWO && pi_money == 2'b01) \|\| (state == TWO &&
pi_money == 2'b10) \|\| (state == ONE_HALF && pi_money == 2'b10))
po_cola <= 1'b1;
else
po_cola <= 1'b0;
//第二段状态机，描述当前状态state和输入pi_money如何影响po_money输出
always@(posedge sys_clk or negedge sys_rst_n)
if(sys_rst_n == 1'b0)
po_money <= 1'b0;
else if((state == TWO) && (pi_money == 2'b10))
po_money <= 1'b1;
else
po_money <= 1'b0;
endmodule

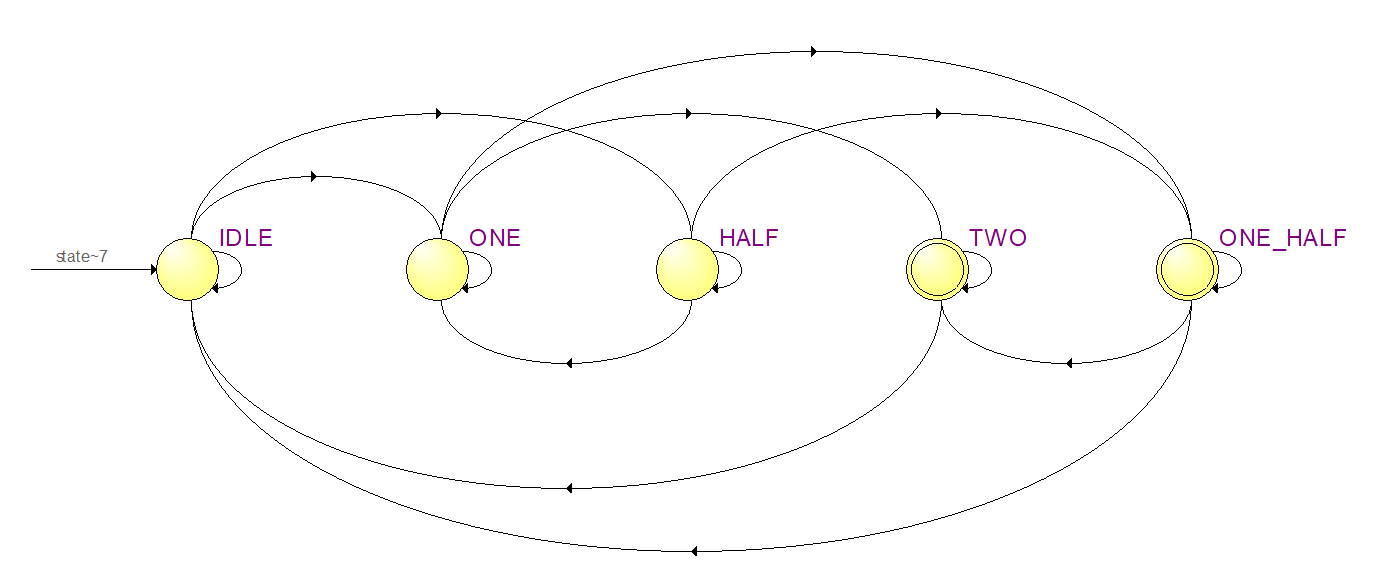
代码编写的方法和上一节中的套路是如出一辙的，我们根据状态转移图按照编写状态机套用的模板很容易就可以编写出状态机的代码。代码编写后综合出的状态转移图如图 23‑26所示。

图 23‑26 综合的状态转移图

17.5.1.3. 仿真验证

仿真文件编写

代码清单 23‑4 复杂可乐机仿真参考代码（tb_complex_fsm.v）

\`timescale 1ns/1ns
module tb_complex_fsm();

////
//\* Parameter and Internal Signal \//
////

//reg define
reg sys_clk;
 reg sys_rst_n;
 reg pi_money_one;
 reg pi_money_half;
 reg random_data_gen;

 //wire define
 wire po_cola;
 wire po_money;

 ////
 //\* Main Code \//
 ////

 //初始化系统时钟、全局复位
 initial begin
 sys_clk = 1'b1;
 sys_rst_n <= 1'b0;
 #20
 sys_rst_n <= 1'b1;
 end

 //sys_clk:模拟系统时钟，每10ns电平翻转一次，周期为20ns，频率为50MHz
 always #10 sys_clk = ~sys_clk;

 //random_data_gen:产生非负随机数0、1
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 random_data_gen <= 1'b0;
 else
 random_data_gen <= {$random} % 2;

 //pi_money_one:模拟投入1元的情况
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 pi_money_one <= 1'b0;
 else
 pi_money_one <= random_data_gen;

 //pi_money_half:模拟投入0.5元的情况
 always@(posedge sys_clk or negedge sys_rst_n)
 if(sys_rst_n == 1'b0)
 pi_money_half <= 1'b0;
 else
 //取反是因为一次只能投一个币，即pi_money_one和pi_money_half不能同时为1
 pi_money_half <= ~random_data_gen;

 //------------------------------------------------------------
 //将RTL模块中的内部信号引入到Testbench模块中进行观察
 wire [4:0] state = complex_fsm_inst.state;
 wire [1:0] pi_money = complex_fsm_inst.pi_money;

 initial begin
 $timeformat(-9, 0, "ns", 6);
 $monitor("@time %t: pi_money_one=%b pi_money_half=%b
 pi_money=%b state=%b po_cola=%b po_money=%b", $time, pi_money_one,
 pi_money_half, pi_money, state, po_cola, po_money);
 end
 //------------------------------------------------------------

 ////
 //\* Instantiation \//
 ////

 //------------------------complex_fsm_inst------------------------
 complex_fsm complex_fsm_inst(
 .sys_clk (sys_clk ), //input sys_clk
 .sys_rst_n (sys_rst_n ), //input sys_rst_n
 .pi_money_one (pi_money_one ), //input pi_money_one
 .pi_money_half (pi_money_half ), //input pi_money_half

 .po_cola (po_cola ), //output po_money
 .po_money (po_money ) //output po_cola
 );

 endmodule

仿真波形分析

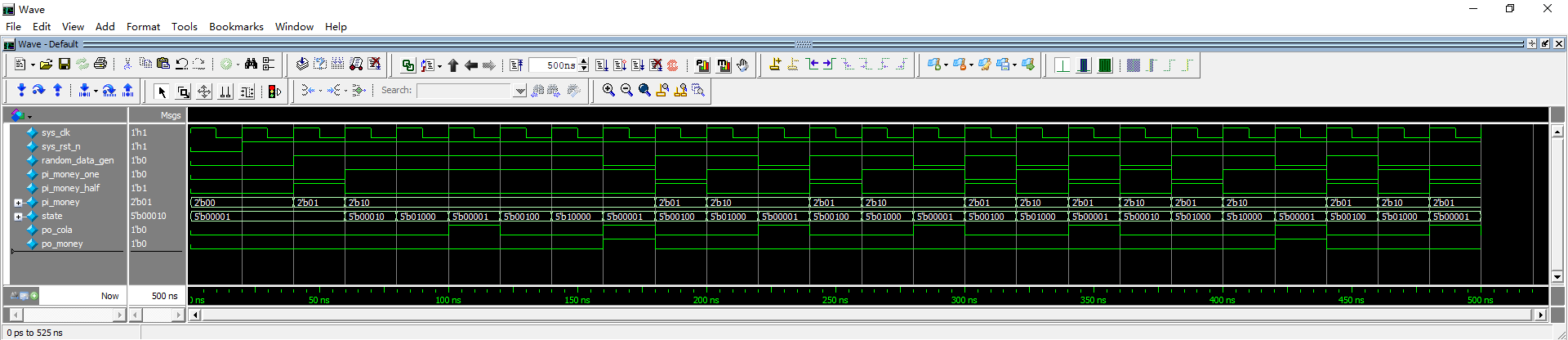
打开ModelSim执行仿真，仿真出来的波形如图 23‑27所示，我们让仿真运行了500ns，可以看到输出信号po_cola和po_money是根据输入信号组合的pi_money和状态变量state共同影响变化的，对照状态转移图和波形图，发现是完全一致的，验证正确。

图 23‑27 仿真波形图

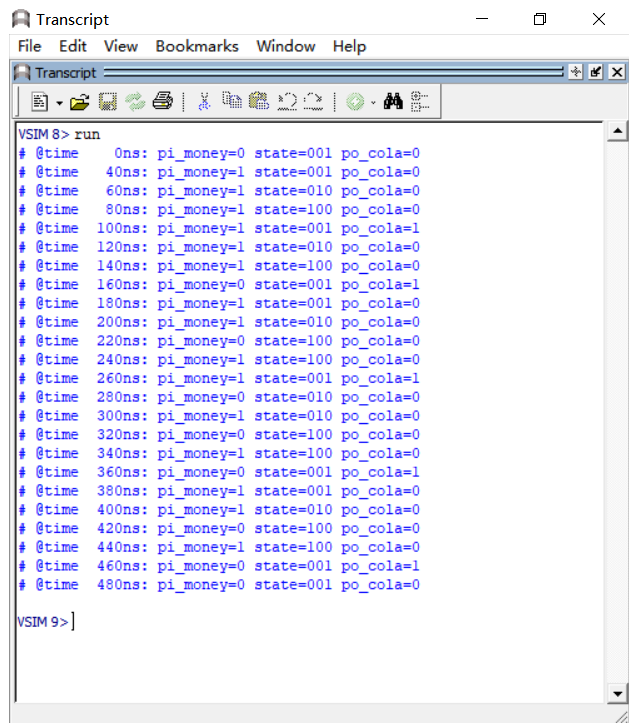
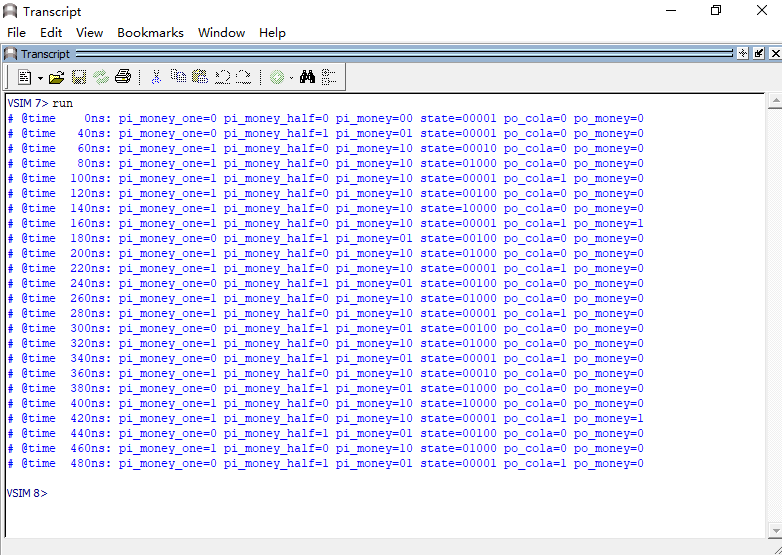
为了方便观察我们依然通过“Transcript”界面打印的信息来查看信号的状态，仿真结果如图 23‑28所示，阅读“Transcript”界面打印的信息时不要忘记时序逻辑电路延一拍的特点，通过和状态转移图的状态和跳转条件进行对比，发现结果是一致的。

图 23‑28 打印信息图

17.6. 章末总结

本章我们通过可乐机的例子详细讲解了状态机的设计方法，一个简单的例子加一个复杂的例子能够让大家对状态机的设计方法得到巩固。本章中讲解的知识点还是很多的，从状态机的概念到状态转移图的设计再到代码的编写和仿真的验证，我们都讲解的非常详细，把设计状态机的方法进行了总结、规范，并将状态机的整体设计步骤总结为以 下四点：

1、首先分析实际问题，然后抽象出我们设计的状态机系统所需要的输入、输出有哪些，以及每个状态都是什么；

2、根据分析绘制状态转移图，状态转移图是可以化简的，我们一般化简到最少状态；

3、根据状态转移图编写代码，代码的编写也是有固定套路的，我们也进行了方法总结；

4、通过综合器综合的状态转移图以及ModelSim仿真验证状态机的设计。

希望大家以后设计新的状态机时能够根据我们总结的步骤一步步分析设计出完美的状态机。状态机虽然好用，但我们也不能编写任何代码时都用状态机去做，虽然理论上可行，但状态机也不是万能的，也有相应的不足，所以我们要在适合状态机应用的场合使用状态机才是最好的。

新语法总结

一般掌握

1、学会将RTL模块中的内部信号引入到Testbench模块中的方法

知识点总结

1、知道状态机是什么，以及适合它的应用场景；

2、了解Moore型状态机和Mealy型状态机的主要区别，以及状态转移图中的差别；

3、学会根据实际问题抽象出我们设计状态机所必要的输入、输出和状态；

4、能够根据分析绘制状态转移图，不要遗漏状态，并会化简、合并状态；

5、能够根据状态转移图画出编写RTL代码，编写代码时也要注意一些细节问题，如：如何进行状态的编码、每种状态编码的特点、我们编写代码的格式、每一段都是做的什么工作；

6、学会根据综合器综合的状态转移图和使用ModelSim仿真来验证我们状态机的设计；

7、记住整个状态机的设计流程、方法、技巧，并能够在以后的设计中熟练运用。

17.7. 拓展训练

前面我们已经学习了很多FPGA相关的知识，包括语法、各种例子，以及相关的波形设计和代码编写方法，这里我们给大家留一个作业，要求以状态机为核心搭建一个小系统。具体要求为：

我们仍以可乐机为背景，一瓶可乐的价格还是2.5元。用按键控制投币（加入按键消抖功能），可以投0.5元硬币和1元硬币，投入0.5元后亮一个灯，投入1元后亮2个灯，投入1.5元后亮3个灯，投入2元后亮4个灯，如果投币后10s不再继续进行投币操作则可乐机回到初始状态。投入2.5元后出可乐不找零，此时led 灯实现单向流水操作，流水10s后自动停止；投入3元后出可乐找零，此时led灯实现双向流水操作，流水10s后自动停止。这里也有复位键，其功能是终止本次投币操作，使可乐机立刻回到初始状态。